Appreciating the geo/S2 library

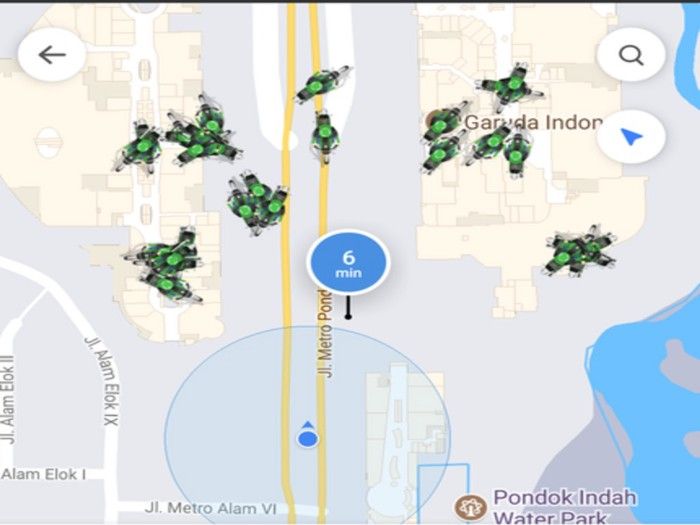
By Shubham Saxena

The home screen of the GO-JEK app looks something like the image above. These are all the available drivers nearby — a function of the earth’s geography.

This article talks about how we use Google’s S2 library to fragment, index and query the earth’s surface to look for nearby drivers. We’ll use the golang version of the library. The original is in Java.

We start by receiving a request from a particular latitude and longitude and convert it into a s2Point using the geo/s2 library. Below:

Our latitude and longitude are the phi and theta angles used to describe a point on a sphere. Given a centre, it’s possible to describe any point on the surface of a sphere with two pieces of information — a latitude and a longitude. For our use case, since the earth’s centre remains constant, we can describe a spherical coordinate with just two variables. Our s2Point is just that; a vector of three floating values(x, y and z coordinates relative to earth’s centre).

Once we have the s2Point, we need the region around that point to look for idle drivers. To do this, we’ll need to project the radius over the surface of the earth and index it. To understand this projection, we’ll need an idea of what spherical caps are.

Sphere cap

Allow me to nerd out a bit. The outer surface of the green portion in the image below is a sphere cap.

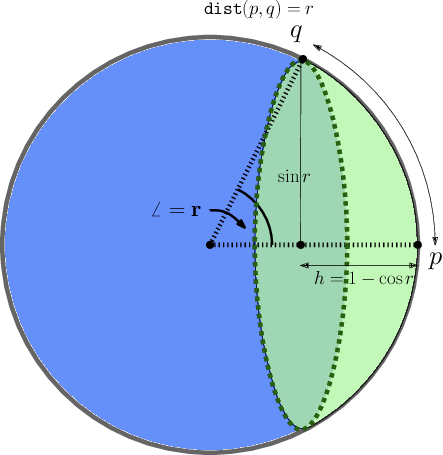
A sphere cap is a portion of a sphere cut out by a plane. For example, a hemisphere is a special case of a sphere cap where the plane passes through the centre.

Let us look at a zoomed-in view of a sphere cap. h becomes significantly smaller when you magnify the point because of the large curvature of the Earth (radius 6371000 metres).

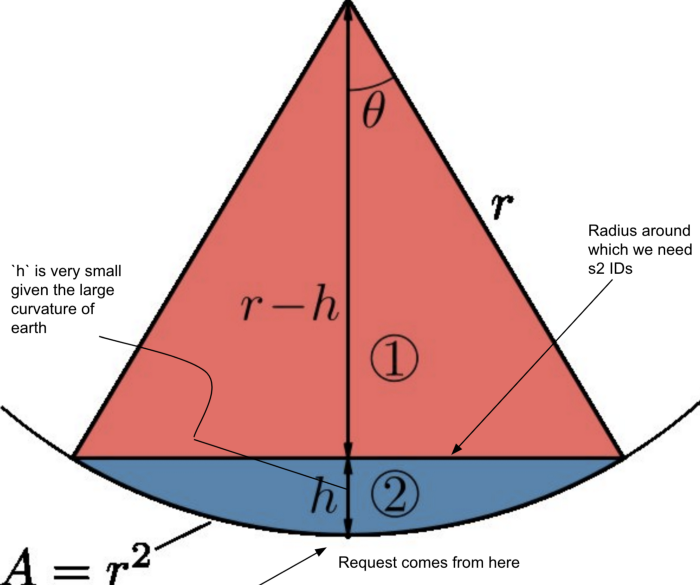
Now, our radius setting ranges from some 1000m to 3000m. These radii are tiny in comparison to the radius of the Earth. At such ratios:

sin(Ω) ~ Ω for Ω --> 0

We’re now in a position to create a spherical cap from the s2Point and the angle(Ω) it projects, given the radius.

This spherical cap is the region we need to query. S2 cells are basically tiny units of geography which allows us to index and query geographical entities such as the spherical cap. These S2 cells have various hierarchal levels which help us define boundaries and sizes according to our requirements.

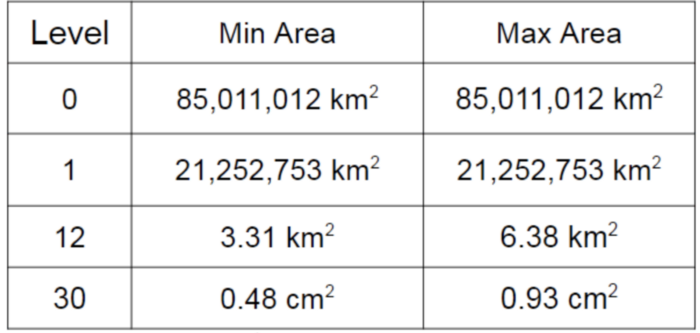
Listed here are some levels and their dimensional specifications for a quick reference.

With the region obtained, we now need to fill it with the required level of s2ID cells. RegionCoverer is a data structure wherein you can specify the maximum number of cells, the maximum cell level and the minimum cell level to be used for covering the 2D region we just generated. It looks something like this:

With the region and the constraints figured out, we use the covering method on RegionCoverer to get hold of the collection of cells that fill it.

Here is the complete function we use to identify nearby S2 cells:

The geo/s2 library provides a simple interface to deal with complex geometries and comes in handy for such use cases. The documentation still lags and I had to do a lot of manual research and code reading to get the grips of it. I hope the article helps you better understand how the underlying engineering works.

Thanks for reading!

References:

• Google’s geo library

Further Reading:

• Is sphere a 2D or 3D mathematical entity?
• How does geo/s2 works